Gráficos estadísticos, medidas de centralización

REPRESENTACIONES GRÁFICAS PARA VARIABLE CUANTITATIVA DE DATOS SIN AGRUPAR 

Diagrama de puntos

Un diagrama de puntos es una gráfica utilizada para ilustrar un número reducido de datos en una distribución unidimensional, son útiles para visualizar la distribución de los datos, la simetría o asimetría, la ubicacción y dispersión de datos.

Por ejemplo:

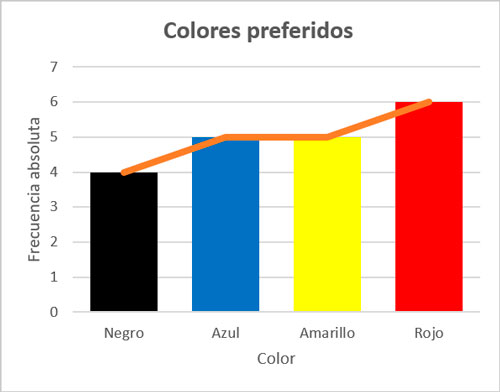
Diagrama de barras 

• Se utiliza para representar datos de VARIABLES DISCRETAS. 
• Se representan en el eje de abscisas los distintos valores de la variable. 
• Sobre cada uno de estos valores se levanta una barra de longitud igual a la frecuencia correspondiente. 
• Se pueden representar tanto las frecuencias absolutas ni como las relativas fi.

Por ejemplo:

Polígono de frecuencias

Se obtiene uniendo con rectas los extremos superiores de las barras del diagrama anterior.

REPRESENTACIONES GRÁFICAS PARA VARIABLE CUANTITATIVA DE DATOS AGRUPADOS

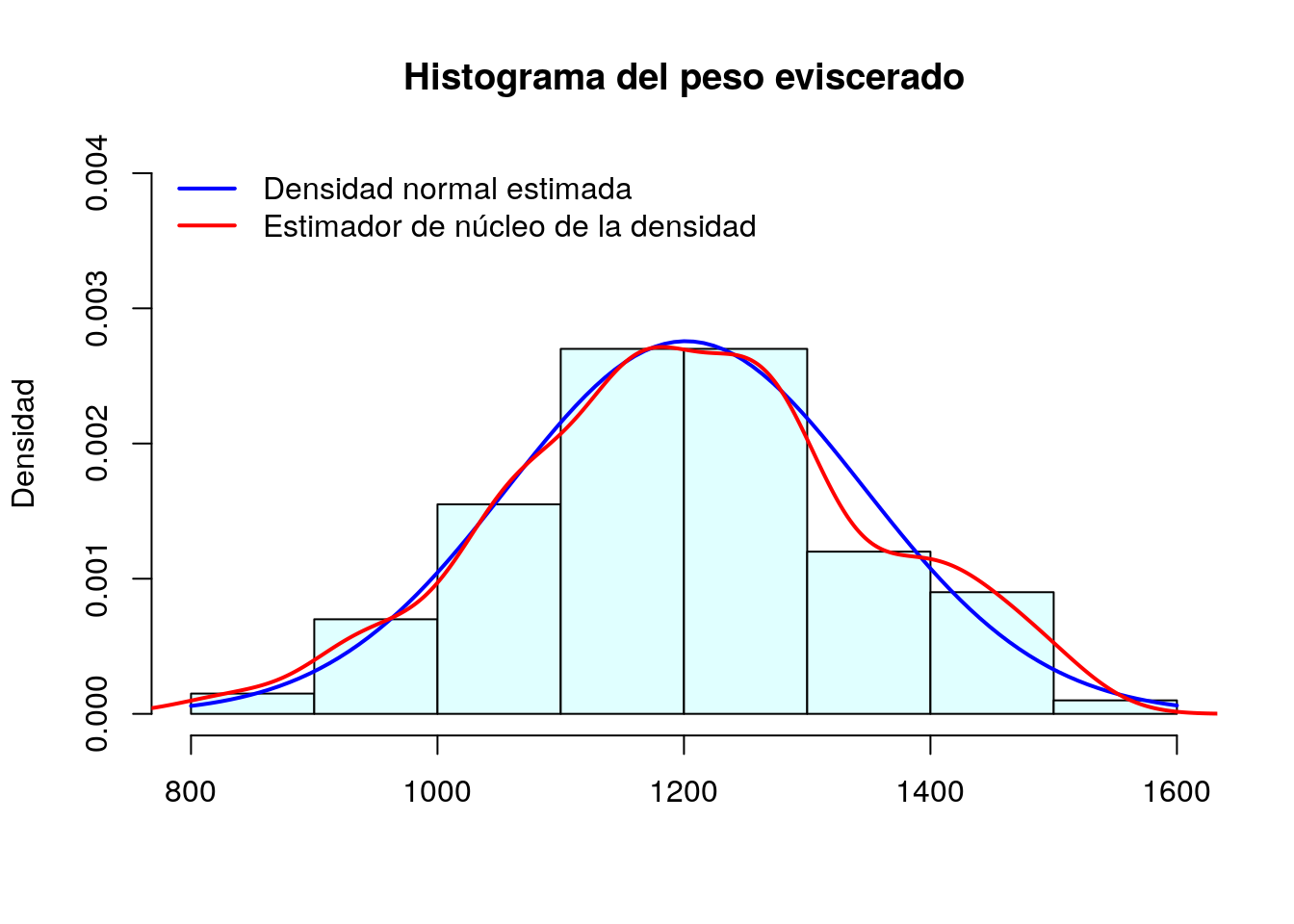
Histograma 

Se utilizan principalmente para datos de variable continua. 

• Es un conjunto de rectángulos adyacentes, cada uno de los cuales representa un intervalo de clase. 
• La base de cada rectángulo es proporcional a la amplitud del intervalo. 
• La altura de cada rectángulo corresponde a la frecuencia absoluta o relativa

Por ejemplo:

Polígono de Frecuencias Acumuladas u Ojiva

Sirve para representar las frecuencias acumuladas de datos agrupados por intervalos. El polígono parte de una altura cero para el extremo inferior del primer intervalo, sobre el extremo superior de cada intervalo se levanta una línea vertical de altura la frecuencia (absoluta o relativa) acumulada de ese intervalo. Evidentemente, la altura que se alcanza al final del polígono es N, para frecuencias absolutas, o 1, para frecuencias relativas.

 REPRESENTACIONES GRÁFICAS PARA VARIABLES CUALITATIVAS 

Existe una gran variedad de representaciones para variables cualitativas, de las cuales vamos a describir las dos más usadas. 

Diagrama de barras o columnas 

Representar en el eje de abscisas las diferentes categorías y levantar sobre cada una de ellas un rectángulo o columna. La altura de cada rectángulo es la frecuencia (absoluta o relativa) de dicha categoría. 

Diagrama de sectores o pastel

Se representa el valor de cada categoría como un sector de un círculo completo. El área de cada sector es proporcional a la frecuencia de la categoría en cuestión. Se multiplica 360◦ por la frecuencia relativa correspondiente. Proporciona una idea visual muy clara de cuáles son las categorías mas representativas.

MEDIDAS DE CENTRALIZACIÓN

Las medidas descriptivas es un conjunto de estadísticas que permiten resumir el comportamiento de un conjunto de datos, entre estas tendremos las medidas de tendencia central, de dispersión y de forma. En el proceso de resumir los datos para describir la información, surgen otros procedimientos englobados en lo que se ha dado por llamar medidas de tendencia central, cuyo objetivo o propósito es hallar un valor tendencia central o categoría que sea “representativo” de todo el conjunto de datos. Este valor “representativo” de las características y atributos de todo el conjunto de datos, es lo que se conoce como el promedio o centro de la distribución de datos. Sin embargo, es muy común observar en libros y publicaciones en general, que dependiendo del área de estudio, por ejemplo, en el campo económico, utilizan la técnica del valor modal para establecer el promedio de los ingresos familiares, o si se revisan aplicaciones en el área de la bioestadística, para establecer el valor promedio de medidas antropométricas, usan el método de la mediana. Así, el valor promedio o central de un conjunto de datos, es un valor que trata de caracterizar o representar a todos los valores de la muestra, y no necesariamente siempre es la media aritmética. El valor central, o simplemente el promedio de la distribución de datos, pueden obtenerse por tres métodos o procedimientos: 

la media aritmética, la mediana, y la moda.

Media aritmética: Se define la media aritmética (o simplemente media) para datos sin agrupar como:

Mediana: Es el valor que divide a la distribución de datos en dos partes iguales. Pero, para establecer tal valor, los datos deben ser primeramente ordenados, ya sea en forma ascendente o descendente. Así, se tiene que de todo el conjunto de datos, el 50 % está por debajo de la mediana, y el otro 50 % está por encima de la mediana. El procedimiento a seguir cuando los datos son individuales es: 

• ordene las n observaciones de menor a mayor. 

• mediana muestral es igual a la observación en la posición n + 1 2 , si n es impar. 

• mediana muestral es igual al promedio de dos observaciones en las posiciones n 2 y n + 2 2 , si n es par. Si los datos están resumidos en intervalos de clase, la mediana se determina por interpolación, así: 

• Se determina la primera clase cuya frecuencia acumulada sea mayor o igual a n 2 dicho intervalo se denomina clase mediana.

Moda: La moda Mo es aquel valor que tiene mayor frecuencia absoluta. Hay ocasiones en las cuales los datos pueden tener dos o más modas, o no puede existir, cuando todos los datos tienen igual frecuencia.